Exploring Titanic passenger data
In this project, a dataset containing details of the passengers on the Titanic is explored and a simple model is built to predict the survival probability of the passengers. Here is the code for this project which was a part of Udacity’s Machine Learning Engineer Nanodegree.
# Import libraries necessary for this projectimport numpy as npimport pandas as pdfrom IPython.display import display # Allows the use of display() for DataFrames
# Import supplementary visualizations code visuals.pyimport visuals as vs
# Pretty display for notebooks%matplotlib inline
# Load the datasetin_file = 'titanic_data.csv'full_data = pd.read_csv(in_file)
# Print the first few entries of the RMS Titanic datadisplay(full_data.head())| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
From a sample of the RMS Titanic data, we can see the various features present for each passenger on the ship:
- Survived: Outcome of survival (0 = No; 1 = Yes)
- Pclass: Socio-economic class (1 = Upper class; 2 = Middle class; 3 = Lower class)
- Name: Name of passenger
- Sex: Sex of the passenger
- Age: Age of the passenger (Some entries contain
NaN) - SibSp: Number of siblings and spouses of the passenger aboard
- Parch: Number of parents and children of the passenger aboard
- Ticket: Ticket number of the passenger
- Fare: Fare paid by the passenger
- Cabin Cabin number of the passenger (Some entries contain
NaN) - Embarked: Port of embarkation of the passenger (C = Cherbourg; Q = Queenstown; S = Southampton)
Since we’re interested in the outcome of survival for each passenger or crew member, we can remove the Survived feature from this dataset and store it as its own separate variable outcomes. We will use these outcomes as our prediction targets.
Run the code cell below to remove Survived as a feature of the dataset and store it in outcomes.
# Store the 'Survived' feature in a new variable and remove it from the datasetoutcomes = full_data['Survived']data = full_data.drop('Survived', axis = 1)
# Show the new dataset with 'Survived' removeddisplay(data.head())| PassengerId | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
The very same sample of the RMS Titanic data now shows the Survived feature removed from the DataFrame. Note that data (the passenger data) and outcomes (the outcomes of survival) are now paired. That means for any passenger data.loc[i], they have the survival outcome outcomes[i].
To measure the performance of our predictions, we need a metric to score our predictions against the true outcomes of survival. Since we are interested in how accurate our predictions are, we will calculate the proportion of passengers where our prediction of their survival is correct. Run the code cell below to create our accuracy_score function and test a prediction on the first five passengers.
Think: Out of the first five passengers, if we predict that all of them survived, what would you expect the accuracy of our predictions to be?
def accuracy_score(truth, pred): """ Returns accuracy score for input truth and predictions. """
# Ensure that the number of predictions matches number of outcomes if len(truth) == len(pred):
# Calculate and return the accuracy as a percent return "Predictions have an accuracy of {:.2f}%.".format((truth == pred).mean()*100)
else: return "Number of predictions does not match number of outcomes!"
# Test the 'accuracy_score' functionpredictions = pd.Series(np.ones(5, dtype = int))print accuracy_score(outcomes[:5], predictions)Predictions have an accuracy of 60.00%.Making Predictions
If we were asked to make a prediction about any passenger aboard the RMS Titanic whom we knew nothing about, then the best prediction we could make would be that they did not survive. This is because we can assume that a majority of the passengers (more than 50%) did not survive the ship sinking.
The predictions_0 function below will always predict that a passenger did not survive.
def predictions_0(data): """ Model with no features. Always predicts a passenger did not survive. """
predictions = [] for _, passenger in data.iterrows():
# Predict the survival of 'passenger' predictions.append(0)
# Return our predictions return pd.Series(predictions)
# Make the predictionspredictions = predictions_0(data)Question 1
Using the RMS Titanic data, how accurate would a prediction be that none of the passengers survived?
Hint: Run the code cell below to see the accuracy of this prediction.
print accuracy_score(outcomes, predictions)Predictions have an accuracy of 61.62%.Answer: Predictions have an accuracy of 61.62%.
Let’s take a look at whether the feature Sex has any indication of survival rates among passengers using the survival_stats function. This function is defined in the titanic_visualizations.py Python script included with this project. The first two parameters passed to the function are the RMS Titanic data and passenger survival outcomes, respectively. The third parameter indicates which feature we want to plot survival statistics across.
Run the code cell below to plot the survival outcomes of passengers based on their sex.
vs.survival_stats(data, outcomes, 'Sex')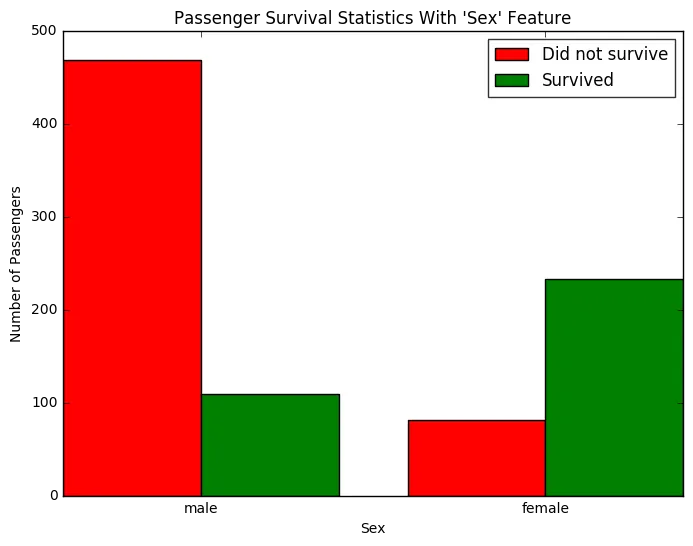
Examining the survival statistics, a large majority of males did not survive the ship sinking. However, a majority of females did survive the ship sinking. Let’s build on our previous prediction: If a passenger was female, then we will predict that they survived. Otherwise, we will predict the passenger did not survive.
Fill in the missing code below so that the function will make this prediction.
Hint: You can access the values of each feature for a passenger like a dictionary. For example, passenger['Sex'] is the sex of the passenger.
def predictions_1(data): """ Model with one feature: - Predict a passenger survived if they are female. """
predictions = [] for _, passenger in data.iterrows():
# Remove the 'pass' statement below # and write your prediction conditions here predictions.append(passenger['Sex'] == "female")
# Return our predictions return pd.Series(predictions)
# Make the predictionspredictions = predictions_1(data)Question 2
How accurate would a prediction be that all female passengers survived and the remaining passengers did not survive?
Hint: Run the code cell below to see the accuracy of this prediction.
print accuracy_score(outcomes, predictions)Predictions have an accuracy of 78.68%.Answer: Predictions have an accuracy of 78.68%.
Using just the Sex feature for each passenger, we are able to increase the accuracy of our predictions by a significant margin. Now, let’s consider using an additional feature to see if we can further improve our predictions. For example, consider all of the male passengers aboard the RMS Titanic: Can we find a subset of those passengers that had a higher rate of survival? Let’s start by looking at the Age of each male, by again using the survival_stats function. This time, we’ll use a fourth parameter to filter out the data so that only passengers with the Sex ‘male’ will be included.
Run the code cell below to plot the survival outcomes of male passengers based on their age.
vs.survival_stats(data, outcomes, 'Age', ["Sex == 'male'"])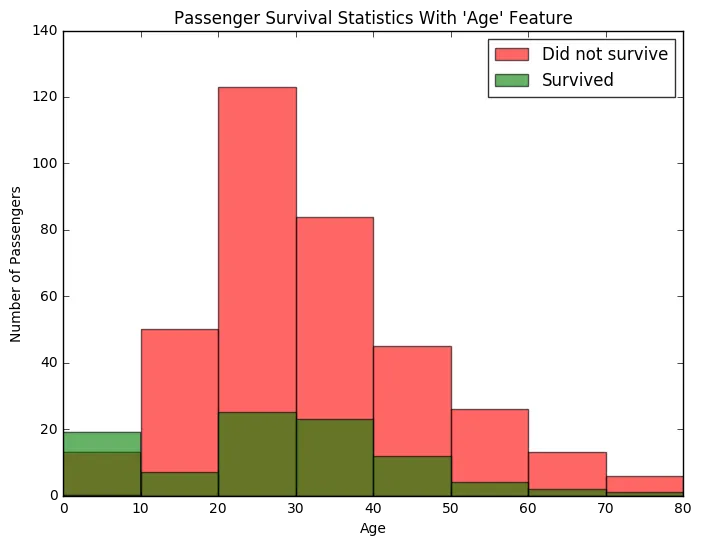
Examining the survival statistics, the majority of males younger than 10 survived the ship sinking, whereas most males age 10 or older did not survive the ship sinking. Let’s continue to build on our previous prediction: If a passenger was female, then we will predict they survive. If a passenger was male and younger than 10, then we will also predict they survive. Otherwise, we will predict they do not survive.
Fill in the missing code below so that the function will make this prediction.
Hint: You can start your implementation of this function using the prediction code you wrote earlier from predictions_1.
def predictions_2(data): """ Model with two features: - Predict a passenger survived if they are female. - Predict a passenger survived if they are male and younger than 10. """
predictions = [] for _, passenger in data.iterrows():
# Remove the 'pass' statement below # and write your prediction conditions here predictions.append(passenger['Sex'] == "female" or (passenger['Sex'] == "male" and passenger['Age'] < 10 ))
# Return our predictions return pd.Series(predictions)
# Make the predictionspredictions = predictions_2(data)Question 3
How accurate would a prediction be that all female passengers and all male passengers younger than 10 survived?
Hint: Run the code cell below to see the accuracy of this prediction.
print accuracy_score(outcomes, predictions)Predictions have an accuracy of 79.35%.Answer: Predictions have an accuracy of 79.35%.
Adding the feature Age as a condition in conjunction with Sex improves the accuracy by a small margin more than with simply using the feature Sex alone. Now it’s your turn: Find a series of features and conditions to split the data on to obtain an outcome prediction accuracy of at least 80%. This may require multiple features and multiple levels of conditional statements to succeed. You can use the same feature multiple times with different conditions.
Pclass, Sex, Age, SibSp, and Parch are some suggested features to try.
Use the survival_stats function below to to examine various survival statistics.
Hint: To use mulitple filter conditions, put each condition in the list passed as the last argument. Example: ["Sex == 'male'", "Age < 18"]
vs.survival_stats(data, outcomes, 'SibSp', ["Sex == 'male'", "Age < 15", "SibSp <= 2"])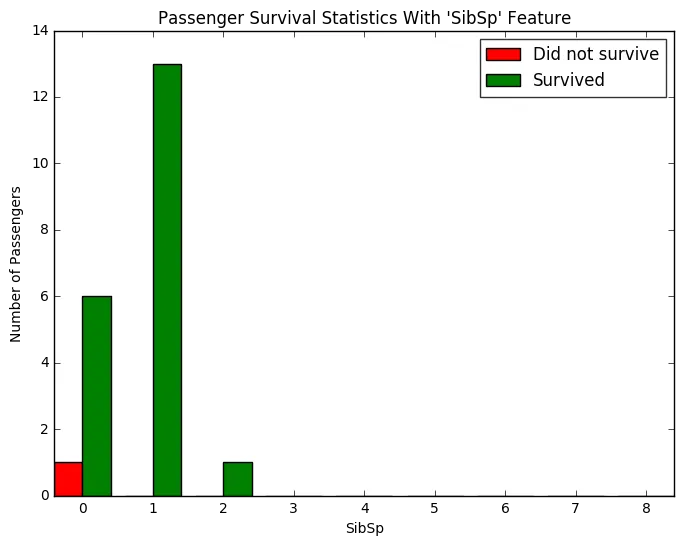
After exploring the survival statistics visualization, fill in the missing code below so that the function will make your prediction.
Make sure to keep track of the various features and conditions you tried before arriving at your final prediction model.
Hint: You can start your implementation of this function using the prediction code you wrote earlier from predictions_2.
def predictions_3(data): """ Model with multiple features. Makes a prediction with an accuracy of at least 80%. """
predictions = [] for _, passenger in data.iterrows():
# Remove the 'pass' statement below # and write your prediction conditions here predictions.append((passenger['Sex'] == "female") or (passenger['Sex'] == "male" and passenger['Age'] < 15 and passenger['SibSp'] <=2))
# Return our predictions return pd.Series(predictions)
# Make the predictionspredictions = predictions_3(data)Question 4
Describe the steps you took to implement the final prediction model so that it got an accuracy of at least 80%. What features did you look at? Were certain features more informative than others? Which conditions did you use to split the survival outcomes in the data? How accurate are your predictions?
Hint: Run the code cell below to see the accuracy of your predictions.
print accuracy_score(outcomes, predictions)Predictions have an accuracy of 80.81%.Answer: Predictions have an accuracy of 80.81%.
Additional features looked at- ‘Pclass’, ‘SibSp’ and ‘Parch’.
I plotted survival stats with the above three features alone while filtering for “‘Sex’ == ‘male’” because most males didn’t survive and it would help to find features that influenced their survival rates.
Number of Siblings/Spouses were more informative than Parch or SibSp for males less than 15 years old.
Above graph clearly shows that most of the males less than 15 years old with at most two siblings survived.
Hence I included this in the prediction model and the accuracy crossed 80%.
Conclusion
After several iterations of exploring and conditioning on the data, you have built a useful algorithm for predicting the survival of each passenger aboard the RMS Titanic. The technique applied in this project is a manual implementation of a simple machine learning model, the decision tree. A decision tree splits a set of data into smaller and smaller groups (called nodes), by one feature at a time. Each time a subset of the data is split, our predictions become more accurate if each of the resulting subgroups are more homogeneous (contain similar labels) than before. The advantage of having a computer do things for us is that it will be more exhaustive and more precise than our manual exploration above. This link provides another introduction into machine learning using a decision tree.
A decision tree is just one of many models that come from supervised learning. In supervised learning, we attempt to use features of the data to predict or model things with objective outcome labels. That is to say, each of our data points has a known outcome value, such as a categorical, discrete label like 'Survived', or a numerical, continuous value like predicting the price of a house.
Question 5
Think of a real-world scenario where supervised learning could be applied. What would be the outcome variable that you are trying to predict? Name two features about the data used in this scenario that might be helpful for making the predictions.
Answer: Supervised learning could be used to predict heart attacks.
Outcome variable would be ‘attacked’ (0- no heart attack, 1- heart attack)
Age, weight, activity levels could be used to make the predictions.
Based on developed prediction model from large data, predictions for new patients could be made.